TL;DR: You can use outputs of intermediate blocks as predictions (usually after adding learned prediction heads). These intermediate blocks’ predictions can then be used to create auxiliary loss terms to be added to the original loss function. Minimizing this new total loss can help create ‘early exits’ in the model, and also improve the full model’s quality via the regularization effect of these auxiliary losses.

---

The Inception paper (Szegedy et al., 2015) had a very neat technique hidden in plain sight, that few people mention: Auxiliarly Losses. They allow you to potentially achieve two nice things:

1. Save model inference costs by only running the model up to a certain number of blocks.
2. Improve the model performance in general.

Let’s jump in to see how we can achieve these two.

Introduction

It might already be intuitive to you, but many recent works are empirically showing that the first few layers of an LLM are doing the heavy lifting when it comes to learning meaningful representations / minimizing the loss, etc. We can exploit this behavior by forcing the model to have an early-exit like behavior, and be depth-competitive.

Informally, if the model has $n$ ‘blocks’, can we get, say $\sim 90\%$ of the performance of the full model with only the first $n/2$ blocks? Additionally can we get $\sim 95\%$ of the full model’s performance with the first $3n/4$ blocks, and so on? The first $n/2$ of the blocks should be the best $n/2$ blocks, the first $3n/4$ blocks should be the best $3n/4$ blocks, etc., i.e. depth-competitive.

Figure 1: A fun illustration of depth-competitive models. (via Gemini)

Let’s slightly formalize the above setting. Assume that the output of the block $i$ is denoted by $z_i$. These are activations at the end of the block $i$, and they encode some meaningful representation of the input. The output of the last block is $z_{n}$ and is transformed to the final output $y_{n}’$. We then minimize the loss $L(y, y_{n}’)$, where $y$ is the ground-truth. $y, z_i,$ and $y_{i}’$ are all tensors of the appropriate dimensions. Refer to Figure 2 for an illustration.

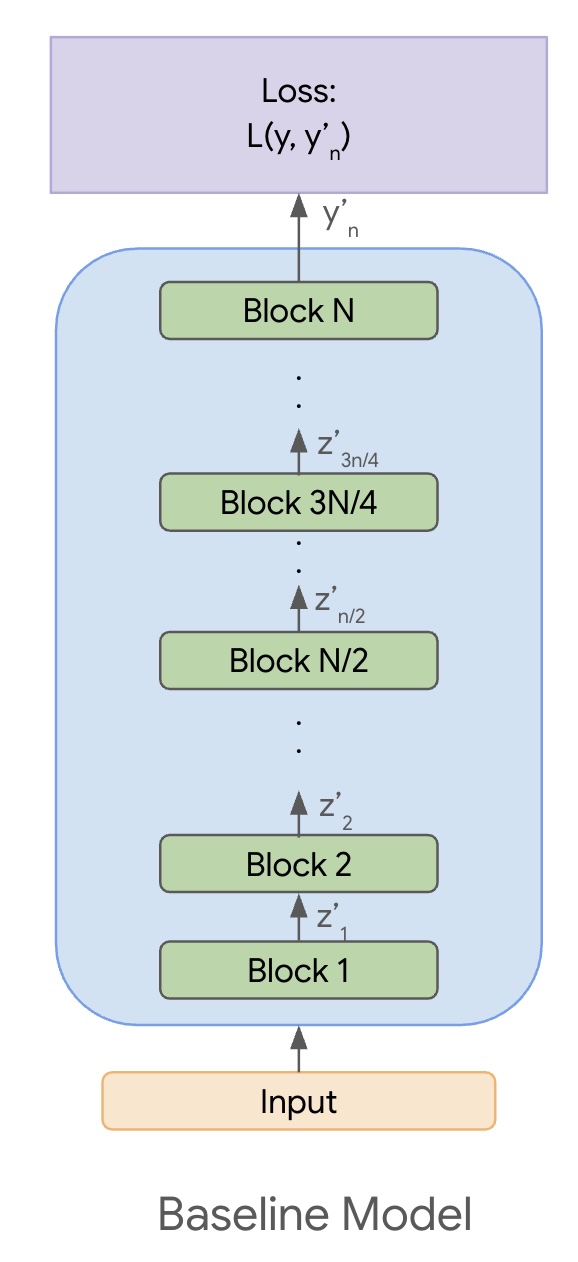
Figure 2: The baseline model consisting of $n$ blocks.

The problem that we have on our hands now is:

1. We have to run the full model to get the output.
2. The intermediate outputs may not make sense for directly predicting the output.

Auxiliary Losses

To solve the above issue, we would like to potentially use the output of the $i$-th block ($z_i$) to generate a prediction. However in many cases $z_i$ cannot be used as-is. For instance, $z_i$ may have a last dimension of size $d$, while the output is expected to be of some other dimension $d’ \neq d$. A simple fix is to attach an auxiliary head, which might simply be a trainable projection matrix $W_i$ such that $y_{i}’ = W_i z_i$, where $y_{i}’$ is the output that we would use for prediction and in the loss.

Additionally, the auxiliary head might anyway be required because the model isn’t trained to generate $z_i$ in such a fashion that it is both: an intermediate representation which is the input to the next block, and also the final output.

Once we have $y_{i}’$ (potentially using auxiliary prediction heads), the auxiliary loss recipe is as follows:

1. Choose the different intermediate depths of the model that we care about, say \(D = \{ 2, n/2, 3n/4 \}\) in this case.
2. Add a loss term $L(y, y_{d}’)$ for each $d \in D$.
3. Optionally add a weight $\alpha_{i}$ (a hyper-param) to tune the contribution of that loss.

So the total loss to be minimized will look as follows:

\[L_{\text{total}} = L(y, y_{n}') + \sum_{d \in D} \alpha_{d} L(y, y_{d}')\]

Refer to Figure 3 below for an illustration of the case where we add auxiliary losses at depths \(D = \{ 2, n/2, 3n/4 \}\).

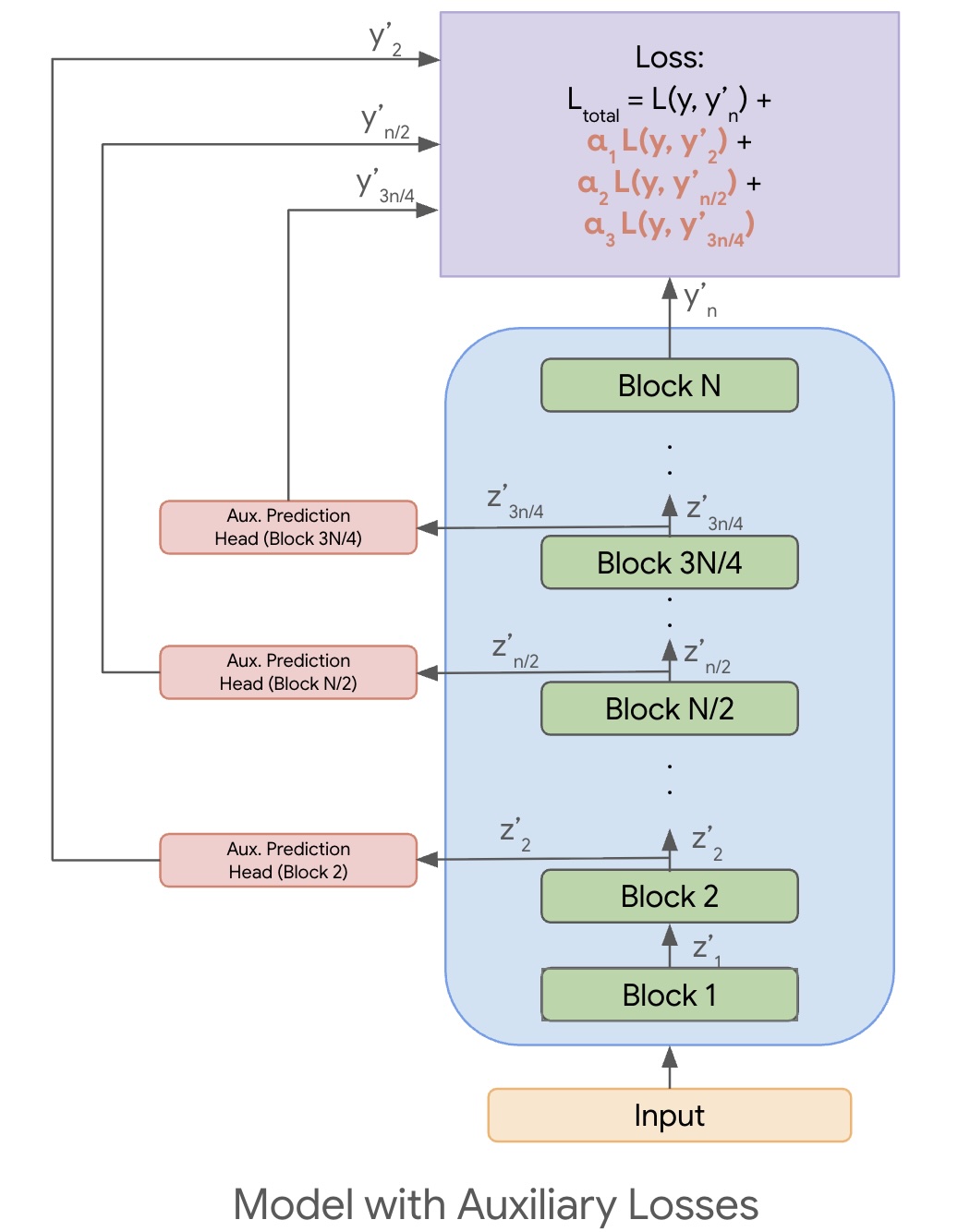
Figure 3: A model with three auxiliary losses at depths $D = \{ 2, n/2, 3n/4 \}$.

Observations

If we minimize the $L_{\text{total}}$ as described above, it will force the model to not just align $y_{n}’$ with $y$, but also the various $y_{d}’$ for each $d \in D$. This will naturally also allow us to use the various $y_{d}’$ as final outputs, where we can adjust the depth $d$ to match our cost v/s quality tradeoff. For example, if we want to get a model that works well with $n/2$ blocks, we would want to add an auxiliary loss term with that depth as described above.

Another nice property is that, even if we don’t intend to use smaller models with $d < n$, auxiliary losses provide a regularizing effect in the model which leads to better model quality, as described in the Inception paper.

If we are only interested in improving the full model’s quality, the auxiliary losses and prediction heads can be added during training, and then discarded during inference.

Conclusion

To summarize, Auxiliary Losses is a simple technique that you can plug into your models to make them depth-competitive, or as a regularizer to just improve model quality.

Thanks to Dhruv Matani for reviewing this post.