Gaurav's Blog
Notes of a Software Engineer - Understand the Problem
23 Nov 2014 - 3 minute read
This is my first post on this blog, which doesn’t discuss any specific problem / technology. As I have been spending time writing code, I feel that it is a good practice to sit back and introspect once in a while. This post has some thoughts, which I hope will make people sit up and notice if they are making the same mistakes. Because this is a long-ish post, some might not read it completely, or some might not be able to relate to the content right now. Regardless, I feel eventually a significant number of us will make the mistakes that I have made in the past, and learn from it first hand. Whatever the case may be, if this makes any sense to you, please share your thoughts and experiences with me :)

As Engineers I feel we are often excited to work on new and ambitious projects. I am specifically talking about non-trivial projects which break new ground, and/or have a reasonable change of not succeeding. The latter could be because it is often the case that, these projects are complicated enough and its hard to be exact with respect to the benefits. These projects might also touch certain areas of the system which are hazy in general.
‘Hazy’ doesn’t really imply that that particular area / part of the system, is naturally hard to understand. It could be just that we don’t know the problem well enough, and how it interacts with those ‘hazy’ areas. I cannot stress enough that it is critical to understand the problem really well before hand. It seems clichéd, and has been repeated so many times, that it will probably not make a good enough impact. So, I will repeat this again in detail, so it stays with you and me, a little longer.
Understand The Problem
As per Prof. Bender, when giving a presentation, making sure that people understand why we did what we did, is the most important thing. Extending this backwards, ever wondered if that problem really needs to be solved in the first place? A lot of times, as a new CS graduate, working on my first full-time unsupervised big tasks, I would really be in awe of the supposed problem. Looking with rose-tinted glasses, you feel that this is what you had told the recruiter and interviewers that you wanted to do in the job. Excellent, lets start working on it. And if you do this, and just jump into this directly, you are going to have a bad time.
Often I did not spend enough time understanding why exactly was I doing what I was doing. Do benchmarks show that this is really needed? Do I have a good enough prototype which shows that if I do what I am going to do, it will give us significant benefits? Do people need this? Has this problem been solved before? What is the minimum I can do to solve this reasonably, and move on to other bigger problems?
This proactive research is what I feel is the difference between new and experienced engineers. In fact, I think, in some cases senior engineers write LESS code than the less experienced ones and still get more things done. Its now clear to me, that the actual coding should only take 10% of the time allocated to the project. If I spend enough time doing my due-diligence and am ‘lazy’, I can simply prune some potential duds much before they turn into huge time sinks. If I spend some more time on the problems which actually require my time, I can figure out things I can do to reduce the scope of the problem, or cleverly use pre-built solutions to do part/most of the work. All this can only come if we (and I will repeat again) Understand. The. Problem.

(Please let me know if you agree or disagree with me about what I said. I would love to hear back).
[0] Sloth picture courtesy: http://en.wikipedia.org/wiki/File:SlothDWA.jpg
Read moreMake an amount N with C coins
11 Oct 2014 - 8 minute read
This week we planned to discuss Dynamic Programming. The idea was to discuss about 4-5 problems, however, the very first problem kept us busy for an entire hour. The problem is a well known one: ‘Given an infinite supply of a set of coin denominations, $C = {c_1, c_2, c_3, …}$, in how many ways can you make an amount N from those coins?’
The first question to be asked is, whether we allow permutations? That is, if, $c_1 + c_2 = N$, is one way, then do we count $c_2 + c_1 = N$, as another way? It makes sense to not allow permutations, and count them all as one. For example, if $N$ = 5, and $C$ = {1, 2, 5}, you can make 5 in the following ways: {1, 1, 1, 1, 1}, {1, 1, 1, 2}, {1, 2, 2}, {5}.
We came up with a simple bottom-up DP. I have written a top-down DP here, since it will align better with the next iteration. The idea was, $f(N) = \sum f(N-c[i])$ for all valid $c[i]$, i.e., the number of ways you can construct $f(5) = f(5-1) + f(5-2) + f(5-5) \implies f(4) + f(3) + f(0)$. $f(0)$ is 1, because you can make $0$ in only one way, by not using any coins (there was a debate as to why $f(0)$ is not 0). With memoisation, this algorithm is $O(NC)$, with $O(N)$ space.
// table stores the results. All values are init to -1.
int table[MAXN];
// cval is the value of coins available.
int cval[MAXC];
// N is the amount, C is the number of coins.
int N, C;
int solve(int n) {
int &res = table[n];
if (res != -1) {
return res;
} else if (n == 0) {
return res = 1;
}
res = 0;
for (int i = 0; i < C; i++) {
if (n - cval[i] >= 0) {
res += solve(n - cval[i]);
}
}
return res;
}
This looks intuitive and correct, but unfortunately it is wrong. Hat tip to Vishwas for pointing out that the answers were wrong, or we would have moved to another problem. See if you can spot the problem before reading ahead.
The problem in the code is, we will count permutations multiple times, for example, for $n = 3$, the result is 3 ({1, 1, 1}, {1, 2} and {2, 1}). {1, 2} and {2, 1} are being treated distinctly. This is not correct. A generic visualization follows.
Assume we start with an amount $n$. We have only two types of coins of worth $1$ and $2$ each. Now, notice, how the recursion tree would form. If we take the coin with denomination $1$ first and the one with denomination $2$ second, we get to a subtree with amount $n-3$, and on the other side, if we take $2$ first, and $1$ next, we get a subtree with the same amount. Both of these would be counted twice with the above solution, even though, the order of the coins does not matter.
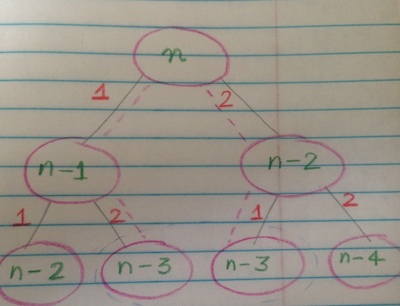
After some discussion, we agreed on a top-down DP which keeps track of which coins to use, and avoids duplication. The idea is to always follow a lexicographic sequence when using the coins. It doesn’t matter if the coins are sorted or not (actually yes, if you check all the coins that you are allowed to use, if they can be used). What matters is, always follow the same sequence. For example, if I have three coins {1, 2, 5}. Let’s say, if I have used coin $i$, I can only use coins $[i, n]$ from now on. So, if I have used coin with value $2$, I can only use $2$ and $5$ in the next steps. The moment I use 5, I can’t use 2 any more.
If you follow, this will allow sequences of coins, in which the coin indices are monotonically increasing, i.e., we won’t encounter a scenario such as {1, 2, 1}. This was done in a top-down DP as follows:
// This is a toy program, so please excuse the trivial flaws.
#define MAXN 2000
#define MAXC 20
// An N*C array, hard-coding the max N = 2000, C = 20.
int r[MAXN][MAXC];
int cval[MAXC];
int N, C;
/**
* O(N*C) solution.
* N is the sum to make, and C is the number of coins you can use. In the method
* n is the amount we have to make, and c denotes the coin number which is the
* smallest coin we can use, i.e., we can only use coins [Cc, Cn-1]. This is to
* prevent double counting.
*/
int solve(int n, int c) {
int &res = r[n][c];
if (res != -1) {
return res;
}
if (n == 0) {
return res = 1;
}
res = 0;
for (int i = c; i < C; i++) {
int rem = n - cval[i];
if (rem >= 0) {
res += f(rem, i);
}
}
return res;
}
int solve(int n) {
memset(r, -1, sizeof(r));
return f(n, 0);
}
Now, this is a fairly standard problem. I decided to check on the interwebs, if my DP skills have been rusty. I found the solution to the same problem on Geeks-for-Geeks, where they present the solution in bottom-up DP fashion. There is also an $O(N)$ space solution in the end, which is very similar to our first faulty solution, with a key difference that the two loops are exchanged. That is we loop over coins in the outer-loop and loop over amount in the inner loop.
int solve(int n) {
int table[1000];
memset(table, 0, sizeof(table));
table[0] = 1;
for (int i = 0; i < C; i++) {
for (int j = cval[i]; j <= n; j++) {
table[j] += table[j - cval[i]];
}
}
return table[n];
}
This is almost magical. Changing the order of the loops fixes the problem. I have worked out the table here step by step. Please let me know if there is a mistake.
Step 1: Calculating with 3 coins, uptil N = 10. Although we use an one-dimensional array, I have added multiple rows, to show how the values change over the iterations.
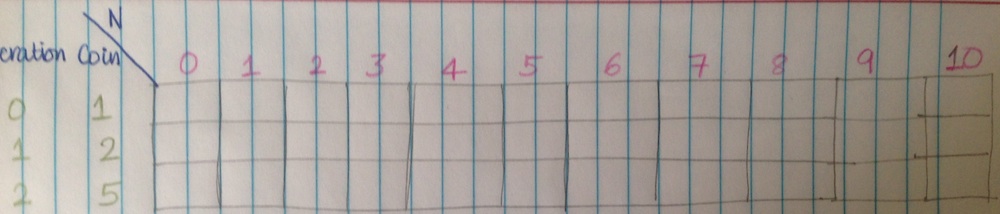
Step 2: Initialize table[0] = 1.
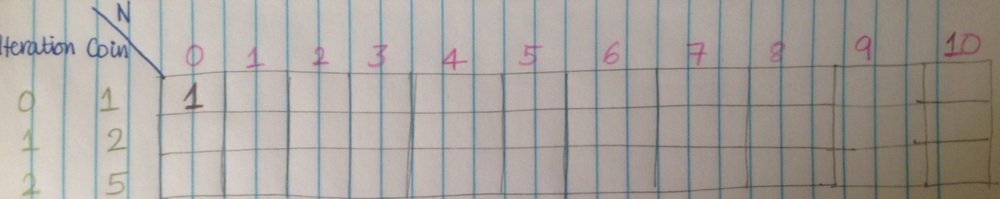
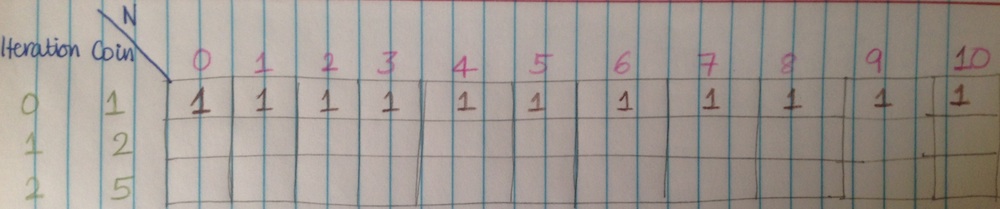
Step 3: Now, we start with coin 1. Only cell 0 has a value. We start filling in values for $n = 1, 2, 3, ..$. Since, all of these can be made by adding \$1 to the amount once less then that amount. Thus, the total number of ways right now, would be 1 for all, since we are using only the first coin, and the only way to construct an amount would be $1 + 1 + 1 + … = n$.
Step 4: Now, we will use coin 2 with denomination \$2. We will start with $n = 2$, since we can’t construct any amount less than \$2 with this coin. Now, the number of ways for making amount \$2 and \$3 would be $2$. One would be the current number of ways, the other would be removing the last two $1$s, and adding a two. Similarily, mentally (or manually, on paper) verify how the answers would be.
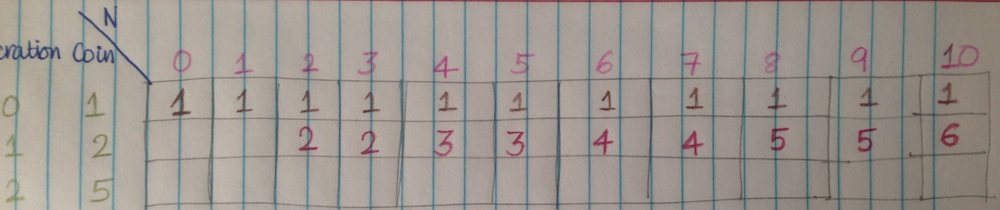
Step 5: We repeat the same for 3. The cells with a dark green bottom are the final values. All others would have been overwritten.
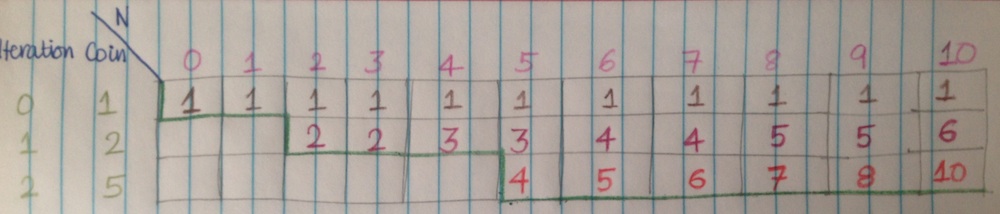
I was looking into where exactly are we maintaining the monotonically increasing order that we wanted in the top-down DP in this solution. It is very subtle, and can be understood, if you verify step 4 on paper, for $4, 5, 6, …$ and see the chains that they form.
In the faulty solution, when we compute amounts in the outer loop, when we reach to amount $n$, we have computed all previous amounts for all possible coins. Now, if you compute from the previous solutions, they have included the counts for all coins. If you try to calculate the count for $n$, using the coin $i$, and result for $n - cval[i]$, it is possible, that the result for $n - cval[i]$, includes the ways with coins > $i$. This is undesirable.
However, when we compute the other way round, we compute for each coin at a time, in that same lexicographical order. So, if we are using the results for $n - cval[i]$, we are sure, that it does not include the count for coins > $i$, because they haven’t been computed yet, since they would only happen after computing the result for $i$.
As they say, sometimes being simple is the hardest thing to do. This was a simple problem, but it still taught me a lot.
Read moreStatic to Dynamic Transformation - I
06 Sep 2014 - 4 minute read
Instead of going into fractal trees directly, I am going to be posting a lot of assorted related material that I am going through. Most of it is joint work with Dhruv and Bhuwan.
This post is about the Static-to-Dynamic Transformation lecture by Jeff Erickson. The motivation behind this exercise is to learn, how can we use a static data-structure, (which uses preprocessing to construct itself and answer queries in future) and create a dynamic data-structure that can continue taking inserts continuously.
I won’t be formal here, so there would be a lot of chinks in the explanation. So either excuse me for that, or read the original notes.
A Decomposable Search Problem
A search problem $Q$ with input $\mathcal{X}$ over data-set $\mathcal{D}$ is said to be decomposable, if, for any pair of disjoint data sets, $D$ and $D’$, the answer over $D \cup D’$, can be computed from the answers over $D$ and $D’$ in constant time. Or:
$Q(x, D \cup D’) = Q(x, D) \diamond Q(x, D’)$
Where $\diamond$ is an associative and commutative function which has the same range, as $Q$. Also, we should be able to compute $\diamond$ in $O(1)$ time. Examples of such a function would be $+$, $\times$, $min$, $max$, $\vee$, $\wedge$ etc. (but not $-$, $\div$, etc.).
Examples of such a decomposable search problem can be a simple existence query, where $Q(x, D$ returns true if $x$ exists in $D$. Then the $\diamond$ function is the binary OR. Another example can be where the dataset is a collection of coordinates, and the query is the number of points which lie in a given rectangle. The $\diamond$ function here is $+$.
Making it Dynamic (Insertions Only)
If we have a static structure that can store $n$ elements by needing $S(n)$ space, after $P(n)$ preprocessing, and can answer a query in $Q(n)$ time. What we mean by a static data-structure is that we can only make inserts into the data-structure exactly once. But we can iterate through that data-structure (this is what the notes have missed, but is a requirement to get the bounds).
Then, we can construct a dynamic data-structure the space requirement of the dynamic structure would be $O(S(n))$, with query time of $O(\log n).Q(n)$, and insert time of $O(\log n).\frac{P(n)}{n}$ amortized.
How do we do this?
Query: Our data-structure has $l$ = $\lfloor{\lg{n}\rfloor}$ levels. Each level $i$ is either empty, or has a static-data structure with $2^i$ elements. Hence, since the search query is decomposable, the answer is simply $Q(D_{0}) \diamond Q(D_{1}) \diamond … \diamond Q(D_{l})$. It is easy to see why the total time taken for the query would be $O(\log n)$ Q(n).
An interesting point is, if $Q(n) > n^\epsilon$, where $\epsilon > 0$ (which essentially means, if $Q(n)$ is polynomial in $n$), then the total query time is $O(Q(n))$. So, for example, if $Q(n) = n^2$, with the static data-structure, the query time with the dynamic data-structure would be $O(Q(n))$. Here is the proof, the total query time is: $\sum{Q(\frac{n}{2^i})} \implies \sum{(\frac{n}{2^i})^\epsilon} \implies n^\epsilon \sum{(\frac{1}{2^i})^\epsilon} \implies n^\epsilon . c \implies O(n^\epsilon) \implies O(Q(n))$ .
Insert: For insertion, we find the smallest empty level $k$, and build $L_k$ with all the preceding levels ($L_0$, $L_1$, …, $L_k$) and the new element, and discard the preceding levels. Since it costs $P(n)$ to build a level, and each element will participate in the array building process $O(\log n)$ times (or jump levels that many times), we will pay the $P(n)$ cost $O(\log n)$ times. Over $n$ elements, that is $O(\log n).\frac{P(n)}{n}$ per element amortized. Again, if $P(n) > n^{1+\epsilon}$ for any $\epsilon > 0$, the amortized insertion time per element is $(O(P(n)/n)$. The proof is similar to what we described above for the query time.
Interesting Tidbit Recollect what we mean when we say that a data-structure is static. A Bloom Filter is a static data-structure in a different way. You can keep inserting elements into it dynamically up to a certain threshold, but you can’t iterate on those elements.
The strategy to make it dynamic is very similar, we start with a reasonably sized bloom-filter, keep inserting into it as long as we can. Once it is too full, we allocate another bloom-filter of twice the size, and insert elements into that, from now on. And so on. The queries are done on all the bloom-filters and are a union of their individual results. An implementation is here.
What Next: Deamortization of this data-structure with insertions as well as deletions. Then we will move on to Cache-Oblivious Lookahead Arrays, Fractional Cascading, and eventually Fractal Trees. This is like a rabbit hole!
Read more