Efficient AI: Auxiliary Losses

21 Aug 2025 - 4 minute read

TL;DR: You can use outputs of intermediate blocks as predictions (usually after adding learned prediction heads). These intermediate blocks’ predictions can then be used to create auxiliary loss terms to be added to the original loss function. Minimizing this new total loss can help create ‘early exits’ in the model, and also improve the full model’s quality via the regularization effect of these auxiliary losses.

The Inception paper (Szegedy et al., 2015) had a very neat technique hidden in plain sight, that few people mention: Auxiliarly Losses. They allow you to potentially achieve two nice things:

1. Save model inference costs by only running the model up to a certain number of blocks.
2. Improve the model performance in general.

Let’s jump in to see how we can achieve these two.

Introduction

It might already be intuitive to you, but many recent works are empirically showing that the first few layers of an LLM are doing the heavy lifting when it comes to learning meaningful representations / minimizing the loss, etc. We can exploit this behavior by forcing the model to have an early-exit like behavior, and be depth-competitive.

Informally, if the model has $n$ ‘blocks’, can we get, say $\sim 90\%$ of the performance of the full model with only the first $n/2$ blocks? Additionally can we get $\sim 95\%$ of the full model’s performance with the first $3n/4$ blocks, and so on? The first $n/2$ of the blocks should be the best $n/2$ blocks, the first $3n/4$ blocks should be the best $3n/4$ blocks, etc., i.e. depth-competitive.

Figure 1: A fun illustration of depth-competitive models. (via Gemini)

Let’s slightly formalize the above setting. Assume that the output of the block $i$ is denoted by $z_i$. These are activations at the end of the block $i$, and they encode some meaningful representation of the input. The output of the last block is $z_{n}$ and is transformed to the final output $y_{n}’$. We then minimize the loss $L(y, y_{n}’)$, where $y$ is the ground-truth. $y, z_i,$ and $y_{i}’$ are all tensors of the appropriate dimensions. Refer to Figure 2 for an illustration.

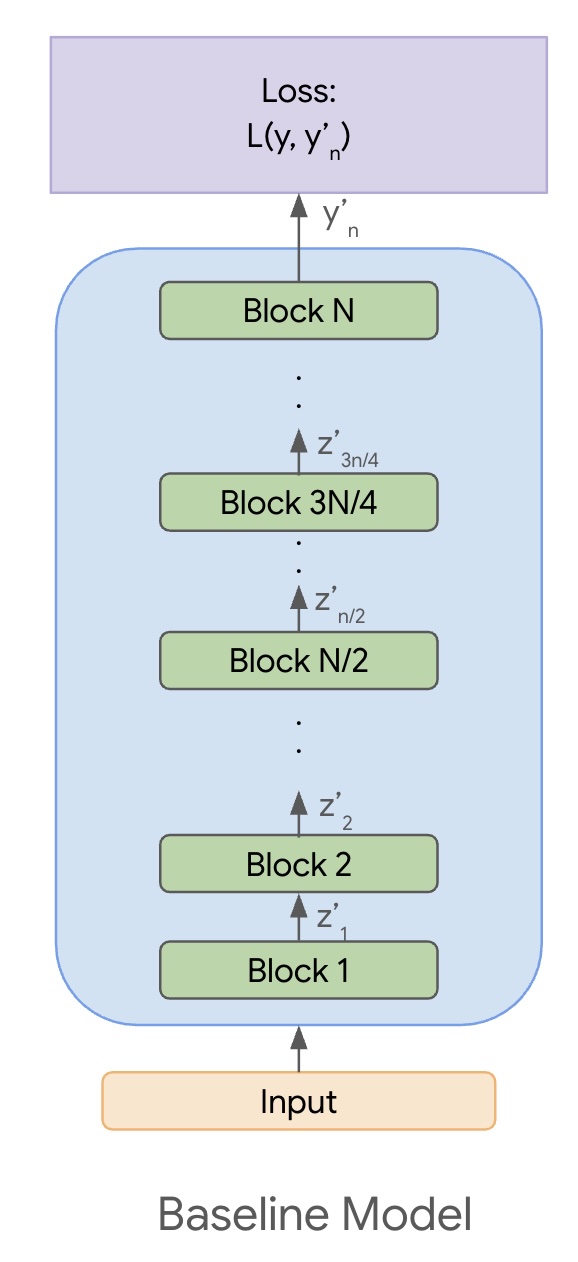
Figure 2: The baseline model consisting of $n$ blocks.

The problem that we have on our hands now is:

1. We have to run the full model to get the output.
2. The intermediate outputs may not make sense for directly predicting the output.

Auxiliary Losses

To solve the above issue, we would like to potentially use the output of the $i$-th block ($z_i$) to generate a prediction. However in many cases $z_i$ cannot be used as-is. For instance, $z_i$ may have a last dimension of size $d$, while the output is expected to be of some other dimension $d’ \neq d$. A simple fix is to attach an auxiliary head, which might simply be a trainable projection matrix $W_i$ such that $y_{i}’ = W_i z_i$, where $y_{i}’$ is the output that we would use for prediction and in the loss.

Additionally, the auxiliary head might anyway be required because the model isn’t trained to generate $z_i$ in such a fashion that it is both: an intermediate representation which is the input to the next block, and also the final output.

Once we have $y_{i}’$ (potentially using auxiliary prediction heads), the auxiliary loss recipe is as follows:

1. Choose the different intermediate depths of the model that we care about, say \(D = \{ 2, n/2, 3n/4 \}\) in this case.
2. Add a loss term $L(y, y_{d}’)$ for each $d \in D$.
3. Optionally add a weight $\alpha_{i}$ (a hyper-param) to tune the contribution of that loss.

So the total loss to be minimized will look as follows:

Refer to Figure 3 below for an illustration of the case where we add auxiliary losses at depths \(D = \{ 2, n/2, 3n/4 \}\).

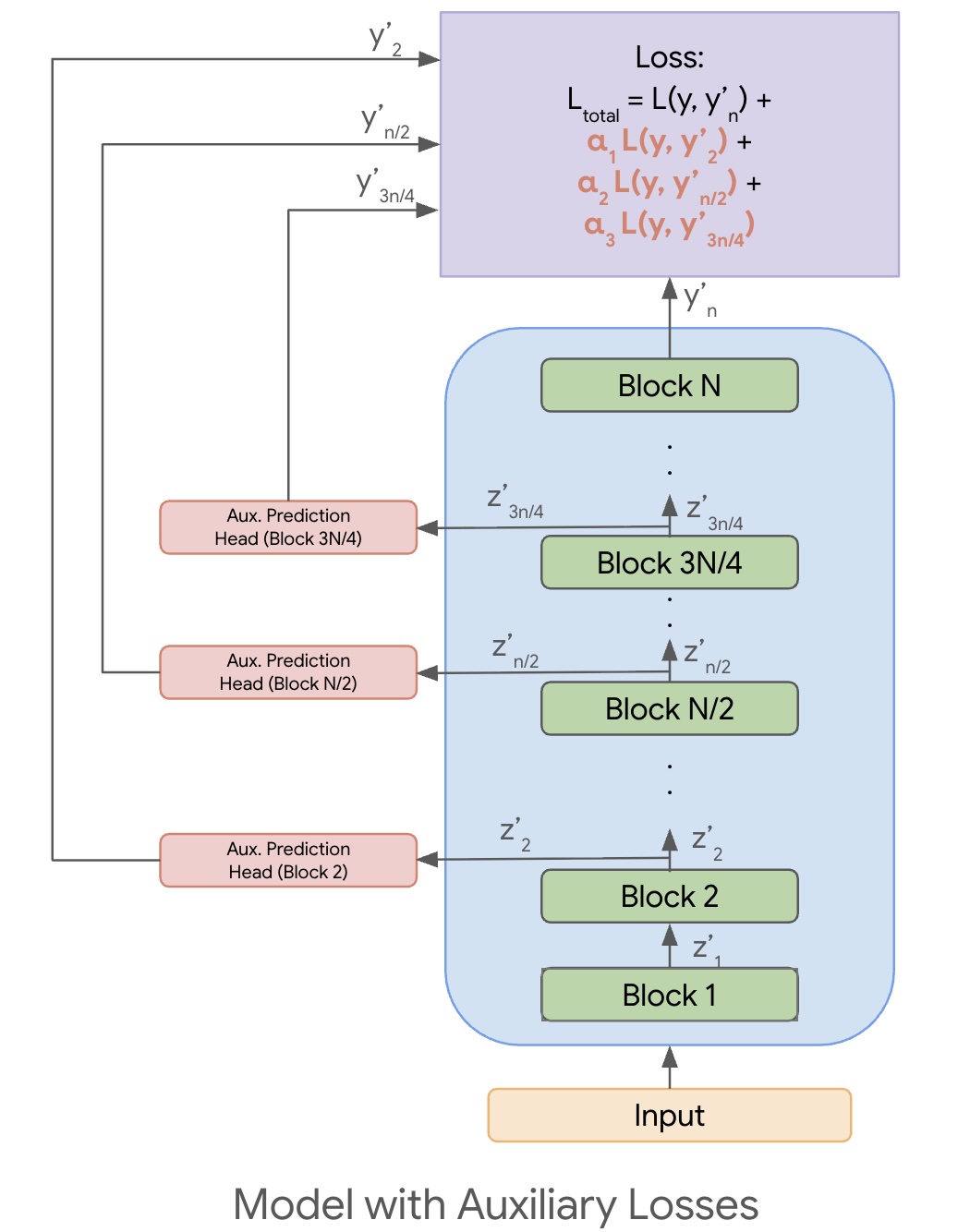
Figure 3: A model with three auxiliary losses at depths $D = \{ 2, n/2, 3n/4 \}$.

Observations

If we minimize the $L_{\text{total}}$ as described above, it will force the model to not just align $y_{n}’$ with $y$, but also the various $y_{d}’$ for each $d \in D$. This will naturally also allow us to use the various $y_{d}’$ as final outputs, where we can adjust the depth $d$ to match our cost v/s quality tradeoff. For example, if we want to get a model that works well with $n/2$ blocks, we would want to add an auxiliary loss term with that depth as described above.

Another nice property is that, even if we don’t intend to use smaller models with $d < n$, auxiliary losses provide a regularizing effect in the model which leads to better model quality, as described in the Inception paper.

If we are only interested in improving the full model’s quality, the auxiliary losses and prediction heads can be added during training, and then discarded during inference.

Conclusion

To summarize, Auxiliary Losses is a simple technique that you can plug into your models to make them depth-competitive, or as a regularizer to just improve model quality.

Thanks to Dhruv Matani for reviewing this post.

'Noam Notation' for Readable Modeling Code

12 Aug 2025 - 3 minute read

This post goes over what people on ML Twitter refer to as the ‘Noam Notation’, (eponymously named after Noam Shazeer, of the Transformer, MoE, Multihead Attention, etc. fame). Noam himself calls the same thing ‘Shape Suffixes’ (more detail in his post here).

Let’s jump into it.

Consider a JAX (or PyTorch, etc.) tensor named inputs. The name itself doesn’t tell you much. If you enable strict typing, Python will force you to specify that it is a JAX Array in the following manner: inputs: jax.Array when passing it as an argument, or as -> jax.Array when returning it from a function.

Now, how about if the the tensor was named inputs_BLD, (when combined with typing inputs_BLD: jax.Array) where the BLD part additionally tells you that:

1. There are three dimensions.
2. The first is B (batch), second is L (length, or sequence), and the third and final one is D (or model).

Now if the convention is strictly followed, the code should pass the following check:

assert inputs.shape == (batch_size, seq_len, d_model)

Where batch_size, seq_len, and d_model are your batch size, sequence length, and model dimension, respectively. Again, if your code strictly follows the notation, you would not need to actually perform the assertion.

Assuming that this invariant holds for all tensors in your code, you can easily tell that the following code is guaranteed to compile:

query_BLHK = jnp.einsum('BLD,DHK->BLHK', inputs_BLD, w_q_DHK)

Here we do a matrix multiply between the inputs_BLD and the w_q_DHK tensors. H here stands for the number of heads, and K stands for the per-head embedding dimension. The exact meaning of those characters should either be easy to guess, or established somewhere in the code or documentation.

Regardless, it is easy to see that the two tensors in the above snippet should be compatible for matrix multiplication in that order, and the output tensor should be of shape [B, H, K]. That’s a lot of useful information!

Now imagine if we suddenly turn off the notation. This is how the above snippet would look:

query = jnp.einsum('BLD,DHK->BLHK', inputs, w_q)

Eww. Right? It’s like we stripped a lot of useful information.

The readability benefits of this notation quickly compounds, especially in a large codebase. For example, see the NanoDO framework’s implementation of Causal Attention and other building blocks of the Transformer model. NanoDO uses the character x as a separator between dimensions (so inputs_BLD becomes inputs_BxLxD), but the motivation remains the same. Although one benefit of using a separator could be that you can use multiple characters to denote a dimension, since without a separator you are limited to 26 dimensions.

To summarize, a non-exhaustive list of what Noam Notation allows you to do is as follows:

1. Infer the semantics of a particular tensor just by reading its name.
2. Avoid compilation bugs.
3. Avoid silent bugs that do something unintentional such as broadcasting.

The last one gives me the chills. It’s much better to use this notation than be sorry after wasting hours / days debugging why your model doesn’t train that well. Give Noam Notation a try the next time you are writing something from scratch.

Let me know how you feel about this idea, or if you have your own neat ways of writing and organizing AI / ML related code.

Efficient AI: KV Caching and KV Sharing

05 Aug 2025 - 6 minute read

Firstly, it feels good to blog again after a seven year hiatus. Secondly, starting with this post, I am starting a series on Efficient AI techniques (architecture, optimization, data, etc.). Most of these posts are going to be focused on techniques for improving autoregressive decoder-only models (LLMs) while also being generally applicable to other models with some tweaks. I also assume that you are familiar with the basics of the transformer architecture (if not, this or this might be good first steps.).

Introduction

Doing inference on transformers can be expensive. Inference latency and memory usage scales linearly with the model depth / number of layers ($l$) in the model. Efforts like Early Exits (Xin et al., 2020; Elbayad et al., 2019) aim to reduce the inference latency by reducing the number of layers used while processing easier tokens (for some definition of ‘easier’), but aren’t trivial to implement. We will cover this in a future post.

In this post, we cover two different, but related techniques:

1. KV Caching: cache and reuse the K, V representations of tokens that are already computed in previous steps. You might already be familiar with his.
2. KV Sharing: share the key and value representations ($K$ and $V$) of tokens across the last half of the layers of a transformer model. Therefore avoiding re-computing them across the last half of the layers. Other weight tensors such as query, MLP, etc. remain non-shared. This is a relatively newer technique.

Discussion

One of the reasons for a naive transformer implemention’s expensive inference is the need to compute the key, and value representations for all the tokens in the given sequence in the Self-Attention module. It looks something like the figure below.

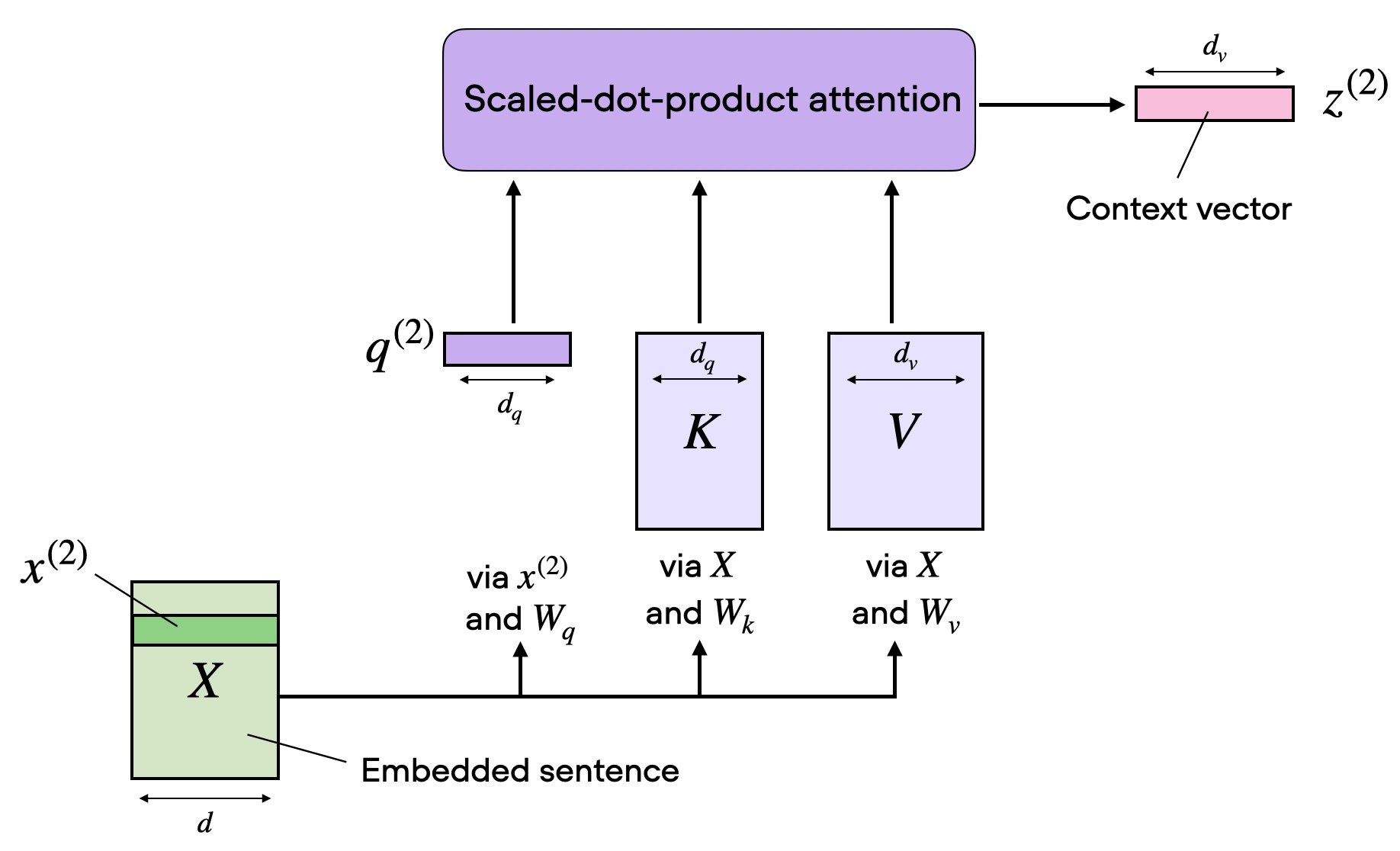
A typical Self-Attention block. Source: Sebastian Raschka's blog.

Since transformers are typically operating in the auto-regressive (AR) setting, this works as follows:

1. Assume we have a sequence of tokens $S = [s_0, s_1, s_2, …, s_{n-1}]$, that we have already generated.
2. To predict the next token, $s_n$, we need the K, V representations of all the tokens in the sequence seen so far. And we need to do this for the $l$ layers.
3. This means we need to compute $l$ matrices of size $(n-1) \times d$, where $d$ is the model dimension / embedding dimension, via a matrix multiplication of the form $X . W_i$, where $X$ is the input at a particular layer, and $W$ is either the key or value weight matrix ($W_K$ or $W_V$) at that layer.
4. This is expensive because we will incur $l$ matrix multiplications, each costing $O(nd^2)$, for a total cost of $O(lnd^2)$ per predicted token! It’s growing faster than the US National Debt!

In the above calculation, we assume a single attention head. Thus the total cost of computing the K,V representations per head ($O(lnd^2)$) is made up of three components:

1. Sequence Dimension: The number of tokens seen so far ($n-1$).
2. Depth Dimension: The number of layers ($l$).
3. Model Dimension: The width of the input stream ($d$).

We can’t do much about $d$ yet, but let’s see how we can tackle the other two for now.

1. KV Caching: Optimizing the sequence dimension.

KV Caching suggests there are two things happening during inference:

• Model weights, including $W_K$ and $W_V$ are fixed.
• K, V representations for a given token $s_i$ only depends on that token and $W_K$ and $W_V$.

Since $W_K$ and $W_V$ are fixed, once we compute the K, V representations for a given (token, layer, head) tuple, it can be reused when predicted any subsequent tokens by caching those representations in memory and reusing them for the next step.

If we can do this, we would only need to compute the K, V representations of the $s_{n-1}$ token when predicting the $n$-th token, since that’s the only token for which we don’t have the K, V vectors. Therefore, it is easy to show that the new total cost of computing the representations is $O(ld^2)$, an $n$-times speedup! This is a significant win, especially if the sequence is very long.

Question: Why don’t we cache the query representation?
Answer: We only compute and use the Q vector of the last token in the Self-Attention block. Thus, there is no need for caching the Q representations for the previous tokens.

2. KV Sharing: Optimizing the depth dimension.

KV Sharing reduces the cost of computing the K, V representations in the depth-dimension ($l$). Concretely, the proposal is that the actual K, V representations are the same between the last half (or any other fraction) of the layers.

Note that we are referring to the actual $K$, $V$ tensors being the same, not just the $W_K$ and $W_V$ matrices being shared. What this means is that the last layer which doesn’t share the K, V representations computes them once, and they are used as is across the remaining half of the layers (regardless of what the inputs are to these layers).

Said in an even simpler way, there is a KV cache across the last half of the layers. This is illustrated in the figure below.

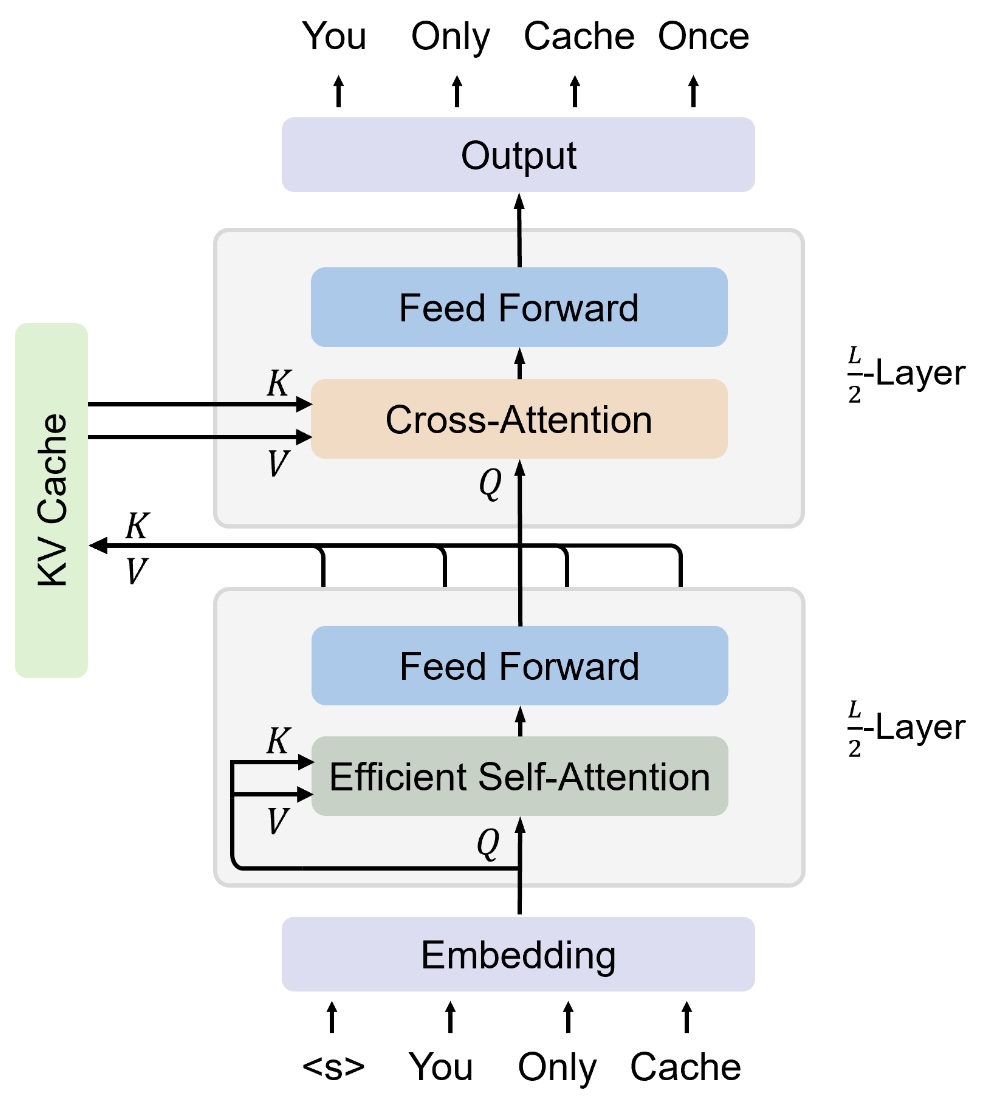
KV Sharing. Source: You Only Cache Once paper.

The figure above illustrates the KV Sharing by showing a shared KV cache between the last $l/2$ layers. It is easy to see that if this works, we can simply not compute the K, V representations for $l/2$ of the layers. More generally, we save $l/k$ of the FLOPS, if the last $l/k$ layers are shared.

However, to make this work we need to ensure that the model is trained with the KV-Sharing behavior. This is detailed in the You Only Cache Once paper.

Some of the intuition behind why this even works in the first place, comes from works like these, which show empirically that in a deep transformer-like model, the last layers are correlated with each other. What this means is that the last few layers are not necessarily adding a lot of new information, but just tweaking the output so far. This redundancy can potentially be exploited (on another note, how can we make these layers do more heavy lifting?).

Additionally, note that we are only sharing the K, V representations, so it only affects the representations of the tokens seen in the past in the Self-Attention block, and is allowing cheap some degrees of freedom to the model.

Another bonus of this technique:

1. You also save a lot of memory, since you don’t have to store $W_K$ and $W_V$ at all.
2. It is applicable during training as well, so you save on inference and memory during training too.

Conclusion

In this post we saw that we can significantly reduce the costs associated with computing the K,V representations in the Self-Attention block using KV Caching and KV Sharing. Concretely, we reduced it by a factor of:

1. $n$ by implementing KV Caching.
2. $l/2$ by implementing KV Sharing across the last $l/2$ layers.

The total cost is now $O(ld^2)$, but with a significantly smaller constant due to KV Sharing. Additionally, KV Sharing eliminates the $W_K$ and $W_V$ matrices for half the layers, which is another huge gain.

That brings us to a the end of this post. Please feel free to drop in any comments if I missed something.