I’ve been reading a few papers related to scaling Stochastic Gradient Descent for large datasets, and wanted to summarize them here.

Large Scale Distributed Deep Networks - Dean et al., 2012 [Link]

• One of the popular papers in this domain, talks about work on a new distributed training framework called DistBelief. Pre-cursor to the distributed training support in Tensorflow.
• Before this work, ideas for doing SGD in a distributed setting restricted the kind of models (convex / sparse gradient updates / smaller models on GPUs with gradient averaging).
• This works describes how to do distributed asynchronous SGD.

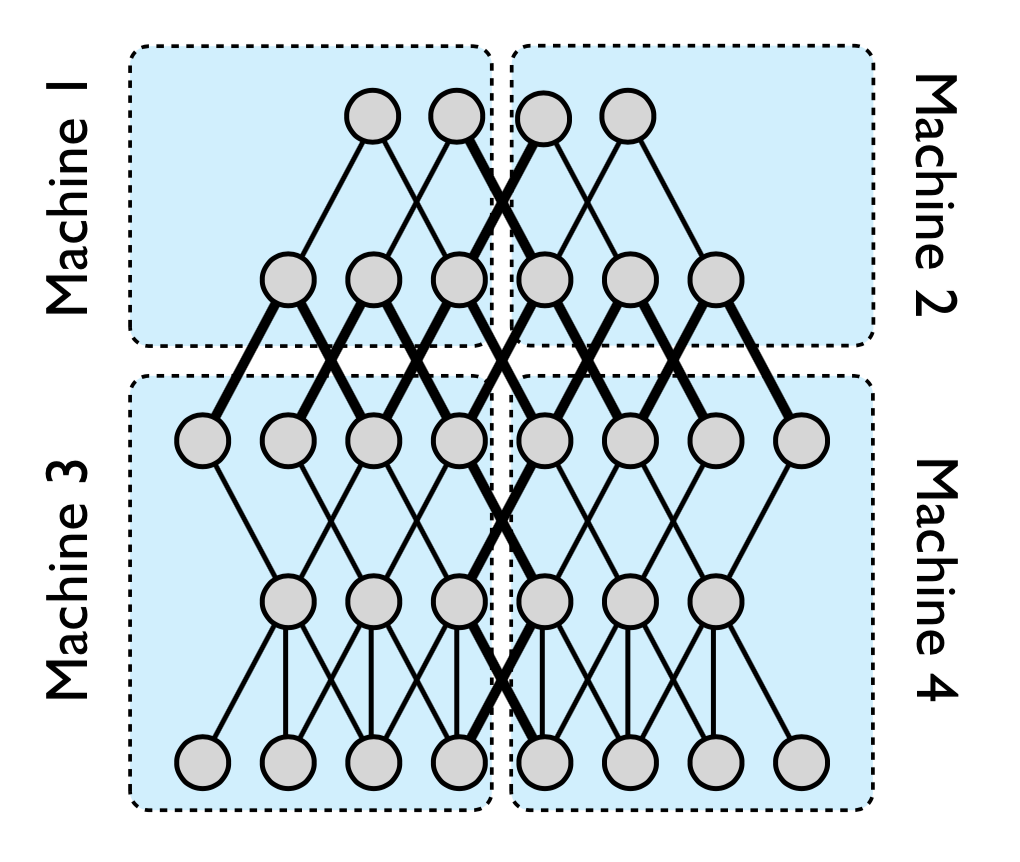
Model-Level Parallelism: Works with large models by splitting the model graph itself into several parts. Each part of the model is assigned to a different machine. If there is an edge between two nodes in different parts, the two machines hosting those parts would need to communicate. This is to get around the problem of fitting a large model on a single GPU.

Downpour SGD: To be able to scale to large datasets, DistBelief also runs several replicas of the model itself. The training data is split into several subsets, and each replica works on a single subset. Each of the replica sends the updates of its params to a Parameter Server. The parameter server itself is sharded, and is responsible for getting updates for a subset of params.

Whenever a new replica starts a new minibatch, it gets the relevant params from the parameter server shards, and then sends its updates when its done with its minibatch.

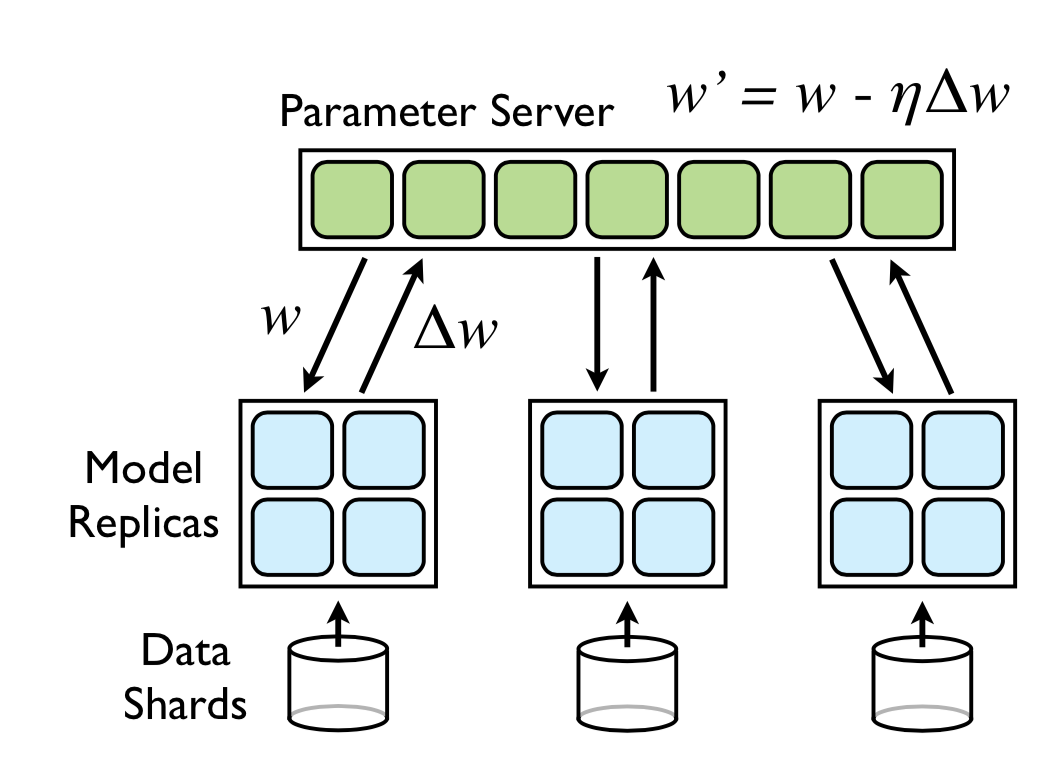
The authors found Adagrad to be useful in the asynchrous SGD setting, since it uses an adaptive learning rate for each parameter, which makes it easy to implement locally per parameter shard.

Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour - Goyal et al. (2017) [Link]

• This paper describes how the authors trained ImageNet using synchronous SGD. However, given the synchronous nature of SGD, the idea is to use large batches (of the order of thousands of samples), instead of mini-batches (which are typically in the tens of samples), to avoid the communication overhead.
• They demonstrate that with their method, they are able to use large batch sizes (up to 8192) without hurting accuracy with a ResNet-50 model (as compared to the baseline model with a batch-size of 256). Using 256 Tesla P100 GPUs, their model trains on the ImageNet dataset within 1 hour.
• Linear Scaling Rule for Learning Rate: “When the minibatch size is multiplied by $k$, multiply the learning rate by $k$.”. One way to think about this is, if the batch size is increased by $k$ times, there are $k$ times fewer updates to weights (since there $k$ times fewer iterations per epoch). Another intuition is, with smaller batches the stochasticity (randomness) of the gradient is higher. With bigger batches, you can confidently take bigger steps.
• The authors do a gradual warm-up of the learning rate from a small value, to the target learning rate, per the linear scaling rule. The authors hypothesize that the linear scaling rule breaks down for large batches in the initial stages of the training, where a gradual warm-up helps with better training.

ImageNet Training in Minutes - You et al. (2018) [Link]

• Another paper that is similar to the paper by Goyal et al. They use a bigger batch-size (32k instead of 8k).
• As per the numbers reported in the paper, with a 32k batch size, they get accuracy comparable to smaller batches. The training finishes in 14 minutes using unspecified number of Intel Knights Landing CPUs (possibly 1024 or 2048).
• They use the gradual warm-up reported in Goyal et al., along with an algorithm that tweaks the learning-rate on a layer-wise basis (LARS algorithm - You et al., 2017). The LARS algorithm is similar to Adagrad (which works on a per-param level), which was useful in Dean et al.’s work.